Modelación de las estructuras diamétricas en bosques naturales de Pueblo Nuevo, Durango
DOI:
https://doi.org/10.29298/rmcf.v13i73.1187Palabras clave:
función Weibull biparamétrica, distribución diamétrica, masas mixtas, método de momentos, recuperación de parámetros, sitios de muestreoResumen
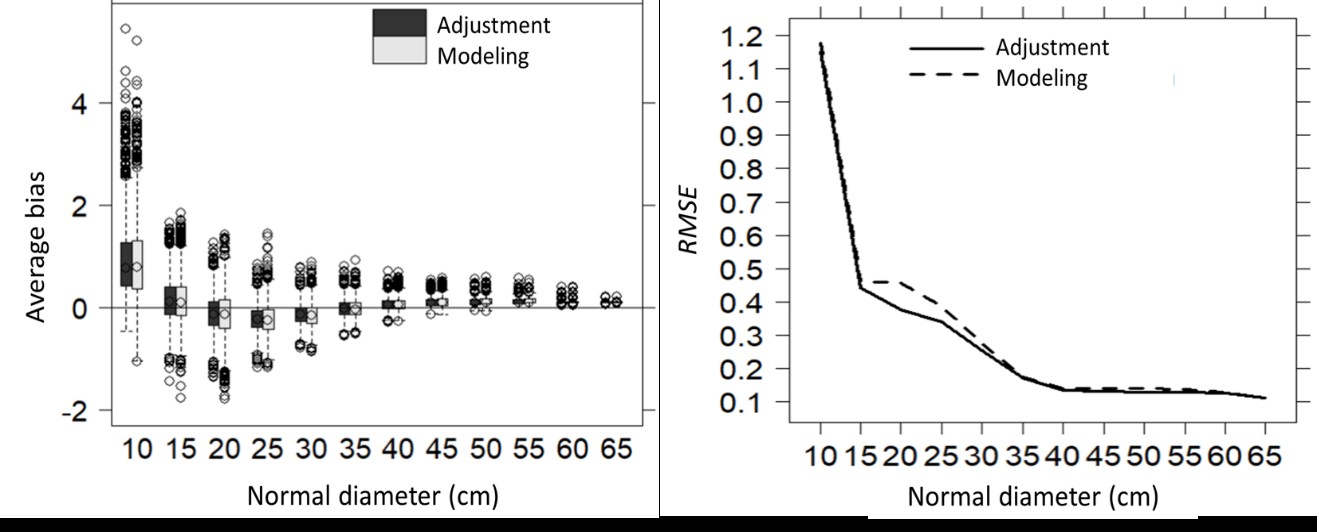
Las distribuciones diamétricas son un factor importante en la caracterización del rodal, ya que el diámetro, generalmente, está correlacionado con otras variables de interés como la altura, volumen, biomasa, etcétera, esto permite conocer el tipo de productos que pueden obtenerse del bosque. El objetivo de la presente investigación fue desarrollar una estrategia para ajustar las FDP Weibull, Beta y SB Johnson, así como reconstruir (modelación) la distribución diamétrica futura con el método de recuperación de parámetros. En una primera etapa, se estudió comparativamente la calidad de ajuste de tres funciones de distribución de probabilidad (FDP: Weibull, SB Johnson y Beta) mediante los métodos de momentos y máxima verosimilitud para recuperar los parámetros y describir la distribución diamétrica de 2 252 parcelas temporales de muestreo, ubicadas en bosques naturales de Pueblo Nuevo, Durango, México. En general, los mejores resultados, en términos de precisión y parsimonia en la etapa de ajuste, evaluados mediante el sesgo medio y la raíz del error medio cuadrático se obtuvieron con la FDP Weibull ajustada con el método de los momentos; mientras que, las distribuciones SB Johnson y Beta se ubicaron en segundo y tercer lugar, respectivamente. Por tanto, la FDP Weibull biparamétrica fue seleccionada para modelar las distribuciones diamétricas de los rodales estudiados. La técnica de la recuperación de parámetros evidenció que 62 % de las parcelas modeladas siguen una distribución teórica tipo Weibull con 20 % de nivel de significancia en la prueba de Kolmogorov-Smirnov.
Descargas
Citas
Assmann, E. 1979. The principles of forest yield study: studies in the organic production, structure, increment and yield of forest stands. Pergamon Press. New York, NY, USA. 506 p.
Bailey, R. L. and T. R, Dell. 1973. Quantifying diameter distributions with the Weibull function. Forest Science 19:97 104. Doi: 10.1093/forestscience/19.2.97.
Cao, Q. V. 2004. Predicting parameters of a Weibull function for modeling diameter distribution. Forest Science 50:682 685. Doi: 10.1093/forestscience/50.5.682.
Corral-Rivas, S., J. G. Álvarez G., J. J. Corral R. and C. A. López S. 2015. Characterization of diameter structures of natural forests of northwest of Durango, Mexico. Revista Chapingo Serie Ciencias Forestales y del Ambiente 21(2):221 236. Doi: 10.5154/r.rchscfa.2014.10.046. DOI: https://doi.org/10.5154/r.rchscfa.2014.10.046
Delignette, M. L. and C. Dutang. 2015. Fitdistrplus: An R package for fitting distributions. Journal of Statistical Software 64(4):1 34. https://www.jstatsoft.org/article/view/v064i04. (20/06/2022). DOI: https://doi.org/10.18637/jss.v064.i04
Frazier, J. R. 1981. Compatible whole-stand and diameter distribution models for loblolly pine. PhD thesis, School of Forestry and Wildlife, Virginia Polytechnic Institute and State University, Blackburg, VA, USA. 125 p.
García, M. E. 1981. Modificaciones al sistema de clasificación climática de Köppen (4ª ed.). Instituto de Geografía, Universidad Nacional Autónoma de México. México, D. F. México. 91 p.
González-Elizondo, M. S., M. González E., J. A. Tena F., L. Ruacho G., y I. L. López E. 2012. Vegetación de la sierra madre occidental, México: Una síntesis. Acta Botánica Mexicana 100:351 403. Doi: 10.21829/abm100.2012.40. DOI: https://doi.org/10.21829/abm100.2012.40
Gorgoso, V. J. J., A. Rojo A., A. Camara O., and U. Diéguez A. 2012. A comparison of estimation methods for fitting Weibull, Johnson’s SB and beta functions to Pinus pinaster, Pinus radiata and Pinus sylvestris stands in northwest Spain. Forest Systems 21(3):446 459. Doi: 10.5424/fs/2012213-02736. DOI: https://doi.org/10.5424/fs/2012213-02736
Gorgoso, V. J. J., Ogana, F. N., and P. O. Ige. 2020. A comparison between derivative and numerical optimization methods used for diameter distribution estimation, Scandinavian Journal of Forest Research 35(3 4):1 9. Doi: 10.1080/02827581.2020.1760343. DOI: https://doi.org/10.1080/02827581.2020.1760343
Hyink, D. M. and J. W. Moser Jr. 1983. A generalized framework for projecting forest yield and stand structure using diameter distributions. Forest Science 29(1):85 95. Doi: 10.1093/forestscience/29.1.85.
Jiang, L. and J. Brooks. 2009. Predicting diameter distributions for young longleaf pine plantations in Southwest Georgia. Southern Journal of Applied Forestry 33:25 28. Doi: 10.1093/sjaf/33.1.25. DOI: https://doi.org/10.1093/sjaf/33.1.25
Johnson, N. L. 1949. Systems of frequency curves generated by methods of translation. Biometrika 36(1):149 176. Doi: 10.2307/2332539. DOI: https://doi.org/10.1093/biomet/36.1-2.149
Lei, Y. 2008. Evaluation of three methods for estimating the Weibull distribution parameters of Chinese pine (Pinus tabulaeformis). Journal of Forest Science 54(12):566 571. http://81.0.228.28/publicFiles/02858.pdf. (25/06/2022). DOI: https://doi.org/10.17221/68/2008-JFS
Liu, C., S. Y. Zhang., Y. Lei., P. F. Newton and L. Zhang. 2004. Evaluation of three methods for predicting diameter distributions of black spruce (Picea mariana) plantations in central Canada. Canadian Journal of Forest Research 34(12):2424 2432. Doi: 10.1139/x04-117. DOI: https://doi.org/10.1139/x04-117
Loetsch, F., F. Zöhrer and K. E. Haller. 1973. Forest inventory 2. Verlagsgesellschaft. BLV. Munich, Germany. 469 p.
Maldonado, D., y J. J. Návar. 2002. Ajuste y predicción de la distribución Weibull a las estructuras diamétricas de plantaciones de pino de Durango, México. Madera y Bosques 8(1):61 72. Doi: 10.21829/myb.2002.811306. DOI: https://doi.org/10.21829/myb.2002.811306
Nanos, N., and G. Montero. 2002. Spatial prediction of diameter distributions models. Forest Ecology and Management 161(1 3):147 158. Doi: 10.1016/S0378-1127(01)00498-4. DOI: https://doi.org/10.1016/S0378-1127(01)00498-4
Ogana, F. N. 2020. A percentile-based estimator for the log-logistic function: Application to forestry. Forestry Studies 72(1):107 120. Doi: 10.2478/fsmu-2020-0009. DOI: https://doi.org/10.2478/fsmu-2020-0009
Palahí, M., T. Pukkala and A. Trasobares. 2006. Modelling the diameter distribution of Pinus sylvestris, Pinus nigra and Pinus halepensis forest stands in Catalonia using the truncated Weibull function. Forestry 79(5):553 562. Doi: 10.1093/forestry/cpl037. DOI: https://doi.org/10.1093/forestry/cpl037
Pece, M. G., C. G. de Benítez y M. J. de Galíndez. 2000. Uso de la función Weibull para modelar distribuciones diamétricas en una plantación de Melia azedarach. Revista Forestal Venezolana 44(2):49 52. https://biblat.unam.mx/es/revista/revista-forestal-venezolana/articulo. (25/06/2022).
Pogoda, P., W. Ochal., and S. Orzel. 2019. Modeling diameter distribution of Black Alder (Alnus glutinosa (L.) Gaertn.) Stands in Poland. Forests 10(5):1 16. Doi: 10.3390/f10050412. DOI: https://doi.org/10.3390/f10050412
Quiñonez, B. G., H. M. P. De los Santos, F. Cruz C., M. A. Velázquez y V. G. Ramírez. 2015. Modelación dinámica de distribuciones diamétricas en masas mezcladas de Pinus en Durango, México. Madera y Bosques 21(2):59 71. Doi: 10.21829/myb.2015.212445. DOI: https://doi.org/10.21829/myb.2015.212445
R Core Team. 2020. R: A language and environment for statistical computing. Vienna: R Foundation for Statistical Computing. https://www.Rproject.org/. (12/05/2020)
Reynolds, M. R., T. E. Burk and W. C. Huang. 1998. Goodness-of-fit tests and model selection procedures for diameter distribution models. Forest Science 34(2):373 399. Doi: 10.1093/forestscience/34.2.373.
Sandoval, S., J. Cancino., R. Rubilar., E. Esquivel., E. Acuña., F. Muñoz. and M. Espinosa. 2012. Probability distributions in high-density dendroenergy plantations. Forest Science 58(6):663 672. Doi: 10.5849/forsci.11-028. DOI: https://doi.org/10.5849/forsci.11-028
Scolforo, J. R. S., F. C. Vitti, R. L. Grisi, F. Acerbi and A. L. De Assis. 2003. SB distribution´s accuracy to represent the diameter distribution of Pinus taeda, through five fitting methods. Forest Ecology and Management 175(1 3):489 496. Doi: 10.1016/S0378-1127(02)00183-4. DOI: https://doi.org/10.1016/S0378-1127(02)00183-4
Secretaría del Medio Ambiente y Recursos Naturales [SEMARNAT]. 2016. Anuario Estadístico de la Producción Forestal. Dirección General de Gestión Forestal y de Suelos. México D.F. https://www.gob.mx/semarnat/documentos/anuarios-estadisticos-forestales (24/60/2022).
Sghaier, T., I. Cañellas., R. Calama and M. Sánchez G. 2016. Modelling diameter distribution of Tetraclinis articulata in Tunisia using normal and Weibull distributions with parameters depending on stand variables. iForest – Biogeosciences and Forestry 9(5):702 709. Doi: 10.3832/ifor1688-008. DOI: https://doi.org/10.3832/ifor1688-008
Shifley, S. R. and E. L. Lentz. 1985. Quick estimation of the three parameter Weibull to describe tree size distributions. Forest Ecology and Management 13(3 4):195 203. Doi: 10.1016/0378-1127(85)90034-9. DOI: https://doi.org/10.1016/0378-1127(85)90034-9
Siipilehto, J. and L. Mehtätalo. 2013. Parameter recovery vs. parameter prediction for the Weibull distribution validated for Scots pine stands in Finland. Silva Fennica 47(4):1 22. Doi: 10.14214/sf.1057. DOI: https://doi.org/10.14214/sf.1057
Sokal, R. and F. Rohlf. 2012. Biometry. The principles and practice of statistics in biological research. 4th edition. W.H. Freeman and Company. NY, USA. 915 p.
Sun, S., Q. V. Cao and T. Cao. 2019. Characterizing diameter distributions for uneven-aged pine-oak mixed forests in the Qinling Mountains of China. Forests 10(7):596. Doi: 10.3390/f10070596. DOI: https://doi.org/10.3390/f10070596
Wang, M. and K. Rennolls. 2005. Tree diameter distribution modeling: Introducing the logit – logistic distribution. Canadian Journal of Forest Research 35(6):1305–1313. Doi: 10.1139/x05-057. DOI: https://doi.org/10.1139/x05-057
Descargas
Publicado
Cómo citar
Número
Sección
Licencia
Derechos de autor 2022 Revista Mexicana de Ciencias Forestales

Esta obra está bajo una licencia internacional Creative Commons Atribución-NoComercial 4.0.
Los autores que publiquen en la Revista Mexicana de Ciencias Forestales aceptan las siguientes condiciones:
De acuerdo con la legislación de derechos de autor, la Revista Mexicana de Ciencias Forestales reconoce y respeta el derecho moral de los autores, así como la titularidad del derecho patrimonial, el cual será cedido a la revista para su difusión en acceso abierto.
Todos los textos publicados por la Revista Mexicana de Ciencias Forestales –sin excepción– se distribuyen amparados bajo la licenciaCreative Commons 4.0 Atribución-No Comercial (CC BY-NC 4.0 Internacional), que permite a terceros utilizar lo publicado siempre que mencionen la autoría del trabajo y a la primera publicación en esta revista. (no permite el uso comercial)
Los autores pueden realizar otros acuerdos contractuales independientes y adicionales para la distribución no exclusiva de la versión del artículo publicado en la Revista Mexicana de Ciencias Forestales (por ejemplo, incluirlo en un repositorio institucional o darlo a conocer en otros medios en papel o electrónicos) siempre que indique clara y explícitamente que el trabajo se publicó por primera vez en la Revista Mexicana de Ciencias Forestales.
Para todo lo anterior, los autores deben remitir el formato de carta-cesión de la propiedad de los derechos de la primera publicación debidamente requisitado y firmado por los autores/as. Este formato debe ser remitido en archivo PDF al correo: editorial.forestal@inifap.gob.mx
Esta obra está bajo una licencia de Creative Commons Reconocimiento-No Comercial 4.0 Internacional.





